________________________________________________________
Codice delle resistenze assiali a 4 bande di colore
Valori standard delle resistenze nelle serie E12 ed E24, si tratta tipicamente di componenti per uso generico che utilizzano quattro colori codificati. L’immagine ne mostra la definizione,
l’esempio riguarda una resistenza da 27 Kohm con tolleranza dal valore nominale del 10%.

La prima e la seconda banda colorata formano il valore base della resistenza, la cifra così ottenuta va moltiplicata per il coefficiente indicato dalla terza banda colorata. Il “K” presente
nell’immagine significa mille, la “M” significa un milione.
Solitamente l’intervallo utile rientra tra 1 ohm (Ω) e 10 Mohm (MΩ), l’uso dei colori argento e viola nella 3° striscia è dunque raro.
La quarta banda indica la tolleranza nel valore rispetto il nominale, nei componenti di basso costo vi sono esclusivamente le opzioni di 5 e 10%.
Non tutte le combinazioni nelle due prime cifre significative trovano corrispondenti essendo la produzione limitata ad un set fisso di valori. Le resistenze di minore costo e maggiore diffusione
sono conformi alla serie E12 che comprende dodici intervalli in una decade, altri componenti di maggior pregio invece adottano la serie E24 che comprende ventiquattro intervalli sempre nello
spazio di una decade.
Di seguito i valori per le serie citate, si rammenti che tali cifre base vanno moltiplicate come da indicazioni fornite nella 3° banda colorata.
|
E12 |
E24 |
|
10 |
10 |
|
11 |
|
|
12 |
12 |
|
13 |
|
|
15 |
15 |
|
16 |
|
|
18 |
18 |
|
20 |
|
|
22 |
22 |
|
24 |
|
|
27 |
27 |
|
30 |
|
|
33 |
33 |
|
36 |
|
|
39 |
39 |
|
43 |
|
|
47 |
47 |
|
51 |
|
|
56 |
56 |
|
62 |
|
|
68 |
68 |
|
75 |
|
|
82 |
82 |
|
91 |
Codice delle resistenze
assiali a 5 bande di colore
Valori standard delle resistenze nelle serie E48
ed E96, si tratta tipicamente di componenti di precisione per uso generico che utilizzano cinque colori codificati.
L’immagine ne mostra la definizione, l’esempio riguarda una resistenza con tolleranza dal valore nominale dell’1%.

La prima, la seconda e la terza banda colorata formano il valore base della resistenza, la cifra così ottenuta va moltiplicata per il coefficiente indicato dalla quarta banda colorata. Il “K”
presente nell’immagine significa mille, la “M” significa un milione.
Solitamente l’intervallo utile rientra tra 1 ohm (Ω) e 10 Mohm (MΩ), l’uso dei colori argento e viola nella 4° striscia è dunque raro. La quinta banda indica la tolleranza nel valore rispetto il
nominale, nei componenti di medio costo vi sono esclusivamente le opzioni di 0,5 / 1 e 2%.
Non tutte le combinazioni nelle tre prime cifre significative trovano corrispondenti essendo la produzione limitata ad un set fisso di valori. Le resistenze di maggiore diffusione sono conformi
alla serie E48 che comprende quarantotto intervalli in una decade, altri componenti di maggior pregio invece adottano la serie E96 che comprende novantasei intervalli sempre nello spazio di una
decade.
Di seguito i valori per le serie citate, si rammenti che tali cifre base vanno moltiplicate come da indicazioni fornite nella 4° banda colorata.
|
E48 |
E96 |
|
10,0 |
10,0 |
|
10,2 |
|
|
10,5 |
10,5 |
|
10,7 |
|
|
11,0 |
11,0 |
|
11,3 |
|
|
11,5 |
11,5 |
|
11,8 |
|
|
12,1 |
12,1 |
|
12,4 |
|
|
12,7 |
12,7 |
|
13,0 |
|
|
13,3 |
13,3 |
|
13,7 |
|
|
14,0 |
14,0 |
|
14,3 |
|
|
14,7 |
14,7 |
|
15,0 |
|
|
15,4 |
15,4 |
|
15,8 |
|
|
16,2 |
16,2 |
|
16,5 |
|
|
16,9 |
16,9 |
|
17,4 |
|
|
17,8 |
17,8 |
|
18,2 |
|
|
18,7 |
18,7 |
|
19,1 |
|
|
19,6 |
19,6 |
|
20,0 |
|
|
20,5 |
20,5 |
|
21,0 |
|
|
21,5 |
21,5 |
|
22,1 |
|
|
22,6 |
22,6 |
|
23,2 |
|
|
23,7 |
23,7 |
|
24,3 |
|
|
24,9 |
24,9 |
|
25,5 |
|
|
26,1 |
26,1 |
|
26,7 |
|
|
27,4 |
27,4 |
|
28,0 |
|
|
28,7 |
28,7 |
|
29,4 |
|
|
30,1 |
30,1 |
|
30,9 |
|
|
31,6 |
31,6 |
|
32,4 |
|
|
33,2 |
33,2 |
|
34,0 |
|
|
34,8 |
34,8 |
|
35,7 |
|
|
36,5 |
36,5 |
|
37,4 |
|
|
38,3 |
38,3 |
|
39,2 |
|
|
40,2 |
40,2 |
|
41,2 |
|
|
42,2 |
42,2 |
|
43,2 |
|
|
44,2 |
44,2 |
|
45,3 |
|
|
46,4 |
46,4 |
|
47,5 |
|
|
48,7 |
48,7 |
|
49,9 |
|
|
51,1 |
51,1 |
|
52,3 |
|
|
53,6 |
53,6 |
|
54,9 |
|
|
56,2 |
56,2 |
|
57,6 |
|
|
59,0 |
59,0 |
|
60,4 |
|
|
61,9 |
61,9 |
|
63,4 |
|
|
64,9 |
64,9 |
|
66,5 |
|
|
68,1 |
68,1 |
|
69,8 |
|
|
71,5 |
71,5 |
|
73,2 |
|
|
75,0 |
75,0 |
|
76,8 |
|
|
78,7 |
78,7 |
|
80,6 |
|
|
82,5 |
82,5 |
|
84,5 |
|
|
86,6 |
86,6 |
|
88,7 |
|
|
90,9 |
90,9 |
|
93,1 |
|
|
95,3 |
95,3 |
|
97,6 |
Codice delle resistenze assiali a 6 bande di colore
Valori standard delle resistenze nelle serie di precisione per uso professionale che utilizzano sei colori codificati. L’immagine ne mostra la definizione, l’esempio riguarda una resistenza con
tolleranza dal valore nominale dell’1% e coefficiente di temperatura di 50 ppm (parti per milione / °C).

________________________________________________________________________________________________________________

________________________________________________________
________________________________________________________



GUIDA CONDENSATORI
http://www.argaudio.it/index_file/Page2678.htm
Vedi anche pagina condensatori su IZ0UPS
http://iz0ups.jimdo.com/elettronica/codice-condensatori/
________________________________________________________
________________________________________________________________________________________________________________
________________________________________________________
________________________________________________________
FORMULE
Legge di Ohm
V = R * I R = V / I I = V / R
Resistenza Elettrica R = ρ * l / S
(resistenza = alla resistività per la lunghezza diviso la sezione)
Corrente I
= ΔQ / Δt
( corrente = alla quantità di carica che passa in una sezione di filo in un’unità di tempo)
Resistenze in Serie Rt = R1 + R2 + R3 …![]()
Resistenze in Parallelo Rt = 1 / (1/R1 + 1/R2 + 1/R3
….) 
Due resistenze in parallelo: Rt = R1 * R2 / (R1 + R2)
Potenza generata P = V * I
(la potenza generata è uguale al prodotto tra tensione e corrente)
Potenza dissipata P = R * I^2 o
P = V * I o P = V^2 / R
(es. da una resistenza) (Watt)
Partitore di Tensione V2 = Vt * R2 / (R1 + R2) (per calcolare la tensione di un
(per calcolare la tensione di un
partitore di tensione, si moltiplica la tensione ai capi del partitore per la resistenza collegata al polo negativo e si divide il tutto per la somma delle due
resistenze)
Partitore di Corrente I1 = It * R2 / (R1 + R2) 
________________________________________________________
http://www.prometheusnow.com/blog/formule-elettronica/#potenza
________________________________________________________________________________________________________________
Potenziale elettrico = V, unità di misura: volt (V)
Corrente = I, unità di
misura: ampere (A)
Resistenza = R, unità di misura: ohm ()
Lavoro = W, unità di
misura: joule (J)
Potenza = P, unità di
misura: Watt (W)
Forza = F,
unità di misura: newton(N)
Distanza = s, unità di misura: metri (m)
Legge di Ohm 
x trovare la corrente: 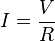
x trovare la resistenza: 
x trovare la tensione: 
________________________________________________________
Potenza e lavoro
x trovare la potenza: 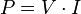


X trovare il lavoro: 


________________________________________________________
https://it.wikibooks.org/wiki/Elettronica_pratica/Formule
________________________________________________________
Legge di Joule
La corrente che attraversa un conduttore di resistenza R produce calore.
La quantità di calore Q è espressa dalla relazione: Q = R·I2 ·t
Se R è espressa in ohm, I in ampere e t in secondi, Q risulta espresso in joule.
Ne segue che la potenza dissipata in watt sarà:
W = R·I2 essendo: W = J/sec
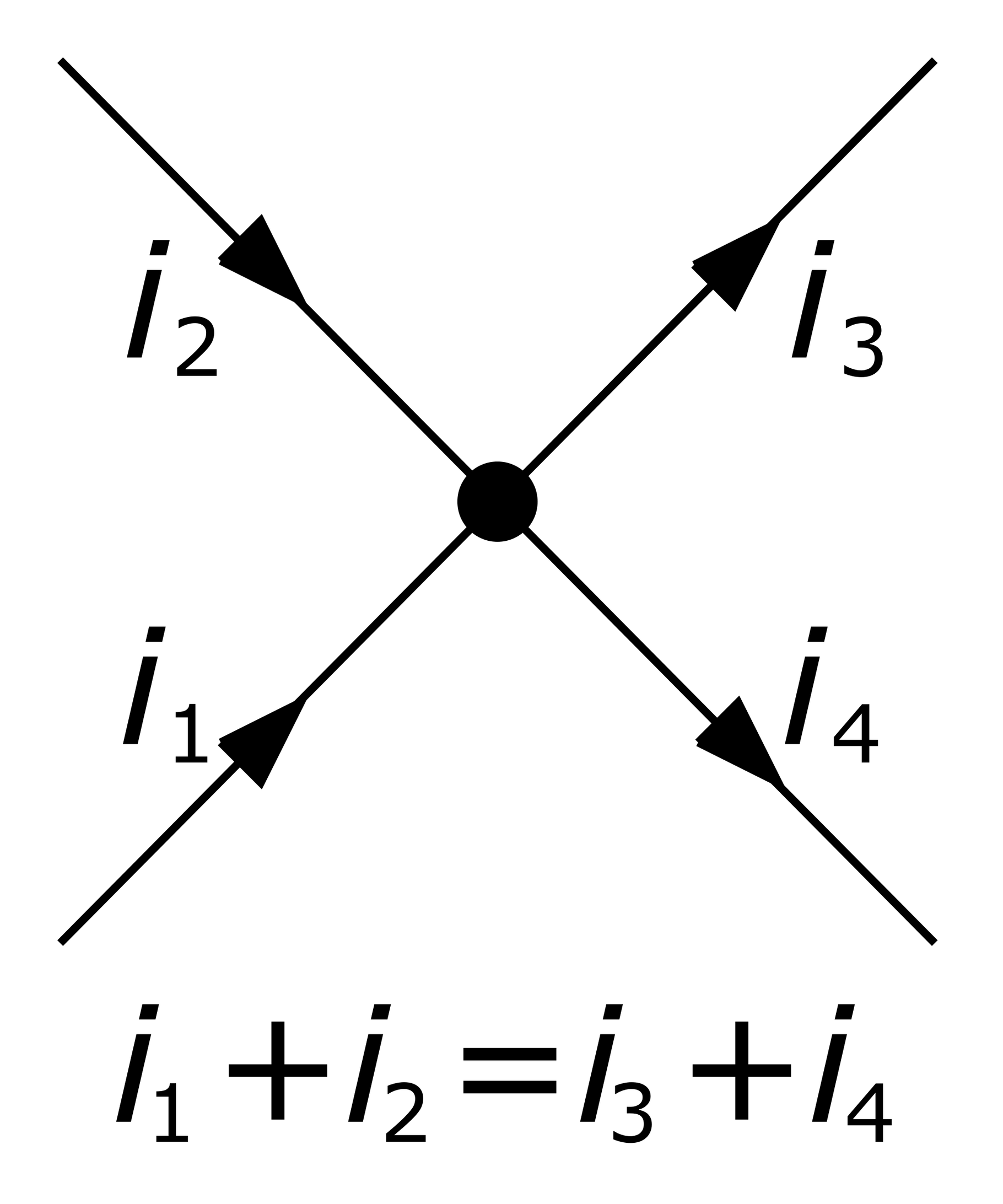
Leggi di Kirchhoff sulle reti
1a – La somma algebrica delle correnti relative ad ogni nodo è uguale a zero: 3I = 0
Ciò significa che la somma delle correnti che affluiscono in un nodo è eguale alla somma delle correnti che se ne allontanano.
2a – La differenza di potenziale tra due punti qualsiasi della rete è indipendente dal cammino lungo la quale essa viene valutata.


________________________________________________________
________________________________________________________
L’impedenza rappresenta la forza di opposizione di un circuito al
passaggio di energia elettrica alternata, e si misura in ohm. Per calcolarla, devi conoscere il valore di tutti i resistori e l’impedenza di tutti gli induttori e condensatori che oppongono una
resistenza variabile al flusso di corrente in base a come questa cambia. Puoi calcolare l’impedenza grazie a una semplice formula matematica.
Riassunto della Formula
- L’impedenza Z = R o XLo XC(se è presente solo uno).
- Impedenza per i soli circuiti in serie Z =
√(R2 + X2) (se R e un tipo di X sono presenti). - Impedenza per i soli circuiti in serie Z =
√(R2 + (|XL – XC|)2) (se R, XL e XC sono tutti presenti). - Impedenza in qualunque tipo di circuito = R +
jX (j è il numero immaginario √(-1)). - Resistenza R = I / ΔV.
- Reattanza induttiva XL = 2πƒL = ωL.
- Reattanza capacitiva XC = 1 / 2πƒL = 1 / ωL.
Calcolare la Resistenza e la Reattanza

1
elettrico o componente. Il risultato ti indica quanto il circuito si oppone al passaggio degli elettroni (cioè alla corrente). Esistono due differenti effetti che rallentano il flusso di corrente
ed entrambi contribuiscono all’impedenza:
- La resistenza (R) è determinata
dalla forma e dal materiale dei componenti. Questo effetto si nota maggiormente con i resistori, ma tutti gli elementi di un circuito hanno un
po’ di resistenza. - La reattanza (X) è determinata
dai campi magnetici ed elettrici che si oppongono ai cambiamenti di corrente o tensione. Si nota maggiormente nei condensatori e induttori.

2
nella Legge di Ohm: ΔV = I * R. Questa equazione ti consente di calcolare uno qualunque dei tre valori conoscendo gli altri due. Ad esempio, per
calcolare la resistenza, puoi riformulare l’equazione secondo i termini R = I / ΔV. Puoi anche misurare la
resistenza grazie a un multimetro.
- ΔV rappresenta la tensione di
corrente, misurata in volt (V). È anche detta differenza di potenziale. - I è l’intensità di corrente e
si misura in ampere (A). - R è la resistenza e si misura
in ohm (Ω).

3
Sappi quale tipo di reattanza devi calcolare. Questa è presente solo nei circuiti a corrente alternata. Proprio come la resistenza, si misura in ohm (Ω).
Esistono due tipi di reattanza che si trovano in diversi componenti elettrici:
- La reattanza induttiva
XL viene generata dagli induttori, chiamati anche bobine. Questi componenti creano un campo magnetico che si oppone ai cambiamenti
direzionali della corrente alternata. Più rapidi sono i cambiamenti direzionali, maggiore è la reattanza induttiva. - La reattanza capacitiva
XC viene prodotta dai condensatori che conservano una carica elettrica. Quando la corrente alternata percorre un circuito e cambia
direzione, il condensatore si carica e scarica ripetutamente. Più il condensatore si deve caricare, più si oppone al flusso di corrente. Per questo motivo, più sono rapidi i cambi direzionali
e minore è la reattanza capacitiva.

4
Calcola la reattanza induttiva. Come descritto in precedenza, questa aumenta con l’aumentare della velocità dei cambi di direzione,
o frequenza del circuito. La frequenza si rappresenta con il simbolo ƒ e si misura in hertz (Hz). La formula completa per
il calcolo della reattanza induttiva è: XL = 2πƒL, dove L è l’induttanza misurata in henry (H).
- L’induttanza L dipende dalle
caratteristiche dell’induttore, come dal numero delle sue spire. È possibile anche misurare l’induttanza in maniera diretta. - Se sei capace di ragionare in
termini di cerchio unitario, immagina la corrente alternata come una circonferenza la cui completa rotazione è pari a 2π radianti. Se moltiplichi questo valore per la frequenza ƒ misurata in
hertz (unità al secondo) ottieni il risultato in radianti per secondo. Questa è la velocità angolare del circuito e viene indicata con la
lettera minuscola omega ω. Puoi anche trovare la formula della reattanza induttiva espressa come XL=ωL.

5
Calcola la reattanza capacitiva. La sua formula è piuttosto simile a quella della reattanza induttiva, tranne per il fatto che quella capacitiva
è inversamente proporzionale alla frequenza. La formula è: XC = 1 / 2πƒC. C è la capacità elettrica o capacitanza del condensatore misurata in farad (F).
________________________________________________________
Calcolare l’Impedenza Totale

1
Somma fra loro tutte le resistenze dello stesso
circuito. Calcolare l’impedenza totale non è difficile, se il circuito ha diversi resistori ma
nessun induttore o condensatore. Per prima cosa misura la resistenza di ogni resistore (o componente che opponga una resistenza), oppure fai riferimento allo schema di circuito per conoscere tali
valori indicati in ohm (Ω). Procedi al calcolo considerando la modalità con cui gli elementi sono collegati:
- Se i resistori sono in serie
(collegati lungo un unico filo secondo un ordine testa-coda), allora puoi sommare fra loro le resistenze. In questo caso la resistenza totale del circuito è R = R1 + R2 + R3… - Se i resistori sono in parallelo
(ciascuno è collegato con un proprio filo allo stesso circuito) allora bisogna sommare i reciproci delle resistenze. La resistenza totale è pari a R = 1 / R1 + 1 / R2 + 1 / R3 …

2
Aggiungi le reattanze simili del circuito. Se sono presenti solo induttori o solo condensatori, l’impedenza è pari alla reattanza totale. Per
calcolarla:
- Se gli induttori sono in serie:
Xtotal = XL1 + XL2 + … - Se i condensatori sono in serie:
Ctotal = XC1 + XC2 + … - Se gli induttori sono in parallelo:
Xtotal = 1 / (1/XL1 + 1/XL2 …) - Se i condensatori sono in
parallelo: Ctotal = 1 / (1/XC1 + 1/XC2 …)

3
Sottrai la reattanza induttiva e capacitiva per avere quella
totale. Dato che queste sono inversamente proporzionali, tendono ad annullarsi l’una con
l’altra. Per trovare la reattanza totale, sottrai il valore minore da quello maggiore.
- Otterrai lo stesso risultato dalla
formula: Xtotal = |XC – XL|.

4
due valori sono “fuori fase”. Questo significa che entrambi i valori cambiano con il tempo in base al ciclo della corrente alternata raggiungendo però i reciproci picchi in momenti diversi. Per
fortuna, se tutti gli elementi sono in serie (collegati dallo stesso filo), puoi usare la semplice formula Z = √(R2 + X2).
- Il concetto matematico alla
base dell’equazione prevede l’utilizzo dei “fasori”, ma puoi dedurla anche per via
geometrica. Puoi rappresentare i due componenti R e X come i cateti di un triangolo rettangolo e l’impedenza Z come l’ipotenusa.

5
conoscenza dei numeri complessi. Questo è anche l’unico modo per calcolare l’impedenza totale di un circuito in parallelo che preveda sia la resistenza che la reattanza.
- Z = R + jX, dove j è il numero
immaginario: √(-1). Si usa j al posto di i per evitare confusione con l’intensità della corrente (I). - Non puoi combinare fra loro i
due numeri. Ad esempio una impedenza deve essere espressa come 60Ω + j120Ω. - Se hai due circuiti come questo
ma in serie, puoi sommare la componente immaginaria con quella reale in maniera separata. Ad esempio, se Z1 = 60Ω + j120Ω ed è in serie con
un resistore con Z2 = 20Ω, allora Ztotale = 80Ω + j120Ω.
________________________________________________________
http://it.wikihow.com/Calcolare-l%27Impedenza
________________________________________________________________________________________________________________